Consider a circular loop of wire of radius a and carrying current I, as shown in fig. Let the plane of the loop be perpendicular to the plane of the paper. We going to find field B at an axial point P at a distance of r from the centre C.
 |
| The magnetic field on the axis of a circular current loop |
Consider a current element dl at the top of the loop. It has an outward coming current.
If s be the position vector of point P relative to the element dl, the Biot-savert law , the field at point P due to the current element is
dB resolved into two rectangular components.
- dBsinΦ along the axis
- dBcosΦ perpendicular to the axis
∴ The total magnetic field at the point P in the direction CP is
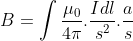
Since μo and I are constant, and s and a is the same for all points on the circular loop, we have
{∵ ∫ dl = circumference=2πa}
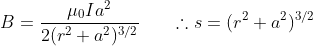
If the coil consists of N turns, then
Special Cases:
- At the centre of the current loop, r =0, therefore
- At the axial points lying far away from the coil, r>>a, so that
- At the axial point at a distance equal to the radius of the coil i.e., r=a, we have
