Magnetic Flux:
The magnetic flux through any surface placed in a magnetic field is the total number of magnetic lines of force crossing this surface normally. It is measure as the product of the component of the magnetic field normal to the surface and the surface area.
Magnetic flux is a scalar quantity, denoted by Ф or ФB. If uniform magnetic field B passes normally through a plane surface area A, then the magnetic flux through this area is
Ф = BA
If the field B makes angle θ with the normal drawn to the area A, as shown in figure then the component of the field normal to this area will be Bcosθ, so that
 |
| Magnetic flux through an area depends on its orientation |
Ф = Bcosθ x A
or Ф = BAcosθ
ϕ=BAcosθ=B→.A→
Note-Unit vector is perpendicular to the area
In general, field B over an area A may not be uniform. However, over a small area element dA, the field B may be assumed to be uniform. As shown in the figure if θ is the angle between and the normal drawn to area element dA, then the component of B normal to dA will be Bcosθ.
 |
| The magnetic field in surface area A |
dϕ=B⊥dA=BcosθdA
=BdAcosθ=B→.dA−→
Then the flux of B through the whole area A is
ϕ=∫AB→.dA−→
The dimension of magnetic flux:
Ф = BA
But B= F/qvsinθ
so Ф = (F/qvsinθ)A
ϕ=MLT−2C.LT−1.L2
[ϕ]=[ML2A−1T−2]
SI unit of magnetic flux:
The SI unit of magnetic flux is weber (wb). One weber is the flux produced when a uniform magnetic field of one tesla acts normally over an area of 1
1weber=1tesla×meter2
1Wb=1Tm2
CGS unit of magnetic flux:
The CGS unit of magnetic flux is Maxwell(Mx). One Maxwell is the flux produced when a uniform magnetic field of one gauss acts normally over an area of 1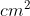
1Mx=1G×cm2
Note:- 1wb=108maxwell
B

