Electric Field At An Axial Point Of A Dipole | cbse24.com

Mohit Rastogi •March 29, 2020

0

The electric field at an axial point of an electric dipole:

As shown in figure an electric dipole consisting of charge +q and -q , separated by distance 2a and placed in a vacuum . Let P be a point on the axial line at distance r from the center O of the dipole on the side of the charge +q.

The electric field at an axial point of a dipole

By this picture, you can see the resultant electric field at an axial point of a dipole this value is 3.51 V/m but if you start increasing distance mean point p on the axial point of dipole than field start decreasing.

The electric field at an axial point of a dipole at a distance

so here you can see that if I increase the distance P on the axial point of a dipole than the electric field start decreasing and its value will be 1.72 V/m. so what I found? , with increasing the distance the electric field will start decreasing.

The electric field at an axial point of a dipole at a far distance

Calculation of the net electric field at an axial point of a dipole:

1. Electric field due to charge -q at point P is

$\overrightarrow{E{-q}}=\frac{-q}{4\pi \varepsilon _{0}(r+a)^{2}}\hat{p}$ ..................(towards left)

2. Electric field due to charge +q at point P is

$\overrightarrow{E{+q}}=\frac{+q}{4\pi \varepsilon _{0}(r-a)^{2}}\hat{p}$ .........................(towards the right)

Note- Where   $\hat{p}$ is the unit vector along the dipole axis from -q to +q

Hence the resultant electric field at point P is

   $\overrightarrow{E_{axial}}=\overrightarrow{E_{-q}}+\overrightarrow{E_{+q}}$

   $\overrightarrow{E_{axial}}=\frac{q}{4\pi \varepsilon _{0}}\times\left ( \frac{1}{(r-a))^{2}}-\frac{1}{(r+a))^{2}} \right )\hat{p}$

   $=\frac{q}{4\pi \varepsilon _{0}} .\frac{4ar}{(r^{2}-a^{2})^{2}}\hat{p}$

or    $\overrightarrow{E_{axial}}=\frac{1}{4\pi \varepsilon _{0}} .\frac{2pr}{(r^{2}-a^{2})^{2}}\hat{p}$

Here P= q x 2a = dip[ole moment .
for r>>a , a2 can be neglected compared to r2

$\overrightarrow{E_{axial}}=\frac{1}{4\pi \varepsilon _{0}} .\frac{2p}{r^{3}}\hat{p}$ .......................(towards right according to vector addition)

Note- The electric field at any point of the dipole acts along the dipole axis from negative to the positive charge i.e in the direction of dipole moment 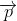$\overrightarrow{p}$ .

Tags: Cbse Class 12 Physics

*

Electric Field At An Axial Point Of A Dipole | cbse24.com

The electric field at an axial point of an electric dipole:

Calculation of the net electric field at an axial point of a dipole:

Contact Form